Unit Circle
Unit Circle: Angles, Radians & Key Coordinates
A unit circle is a circle with a radius of 1 centered at the origin (0,0) on the Cartesian coordinate plane. Because its radius is 1, the coordinates of any point on the circle give the direct values for the sine and cosine of the angle it corresponds to.
The unit circle allows you to move from familiar right-triangle definitions of trigonometric functions into circular definitions. Sine, cosine, and other trig functions can be evaluated for many angles beyond right triangles.
It ties angle measures (in degrees or radians), coordinates (x, y), and the trigonometric functions into one model.
On the unit circle:
- x = cos(θ)
- y = sin(θ)
- Because the radius is 1, the point (x, y) satisfies x² + y² = 1
Degrees vs. Radians
Degrees
- A full revolution is 360°.
- A right angle is 90°.
- Half a circle is 180°.
- Three-quarters of a circle is 270°.
Radians
A radian is an angle measure based on the circle’s radius:
One radian is the angle that cuts off an arc whose length equals the radius.
- A full revolution = 2π radians = 360°
- Therefore: π radians = 180°
Conversion Formulas
- Degrees → radians: radians = degrees × (π / 180)
- Radians → degrees: degrees = radians × (180 / π)
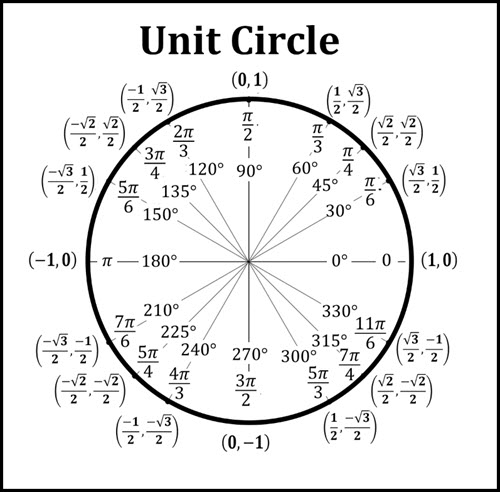
Key Coordinates and Special Angles
How to Use the Unit Circle to Evaluate Trigonometric Functions
- Locate the angle on the unit circle (in degrees or radians).
- Determine the quadrant (I, II, III, IV).
- Sine (y) and cosine (x) change signs depending on the quadrant.
- Read off the coordinate (x, y).
Then:
- cos(θ) = x
- sin(θ) = y
- tan(θ) = y / x, if x ≠ 0
Use exact values like √2/2 or √3/2 for special angles.
For angles outside the first quadrant, apply the sign rules:
- Sine is positive in I & II
- Sine is negative in III & IV
- Cosine is positive in I & IV
- Cosine is negative in II & III
Trigonometric Table
The trigonometric table provides the values of the six basic trigonometric functions, sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot), for the most commonly used angles on the unit circle.
| Angle (°) | Angle (rad) | sin | cos | tan | csc | sec | cot |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | – | 1 | – |
| 30° | π/6 | 1/2 | √3/2 | √3/3 | 2 | 2√3/3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 2√3/3 | 2 | √3/3 |
| 90° | π/2 | 1 | 0 | – | 1 | – | 0 |
| 120° | 2π/3 | √3/2 | -1/2 | -√3 | 2√3/3 | -2 | -√3/3 |
| 135° | 3π/4 | √2/2 | -√2/2 | -1 | √2 | -√2 | -1 |
| 150° | 5π/6 | 1/2 | -√3/2 | -√3/3 | 2 | -2√3/3 | -√3 |
| 180° | π | 0 | -1 | 0 | – | -1 | – |
| 210° | 7π/6 | -1/2 | -√3/2 | √3/3 | -2 | -2√3/3 | √3 |
| 225° | 5π/4 | -√2/2 | -√2/2 | 1 | -√2 | -√2 | 1 |
| 240° | 4π/3 | -√3/2 | -1/2 | √3 | -2√3/3 | -2 | √3/3 |
| 270° | 3π/2 | -1 | 0 | – | -1 | – | 0 |
| 300° | 5π/3 | -√3/2 | 1/2 | -√3 | -2√3/3 | 2 | -√3/3 |
| 315° | 7π/4 | -√2/2 | √2/2 | -1 | -√2 | √2 | -1 |
| 330° | 11π/6 | -1/2 | √3/2 | -√3/3 | -2 | 2√3/3 | -√3 |
| 360° | 2π | 0 | 1 | 0 | – | 1 | – |
Examples
Example 1: Evaluate sin(150°)
150° = 180° – 30°, so it lies in Quadrant II (where x is negative and y is positive). The reference angle is 30°. On the unit circle, the sine of 30° is 1/2.
So: sin(150°) = +1/2
Example 2: Evaluate cos(7π/6)
7π/6 = 210° (π = 180°, so π/6 = 30°, and 180° + 30° = 210°)
210° lies in Quadrant III (both x and y are negative). The reference angle is 30°. The cosine of 30° is √3/2, but negative in this quadrant.
So: cos(7π/6) = -√3/2
Summary
The unit circle is essential for understanding trigonometric functions for all angles, not just acute ones.
On a circle of radius 1, coordinates directly give cos(θ) and sin(θ).
Knowing how to convert between degrees and radians is critical when using the unit circle.
Memorize the special angles (30°, 45°, 60°, etc.) and their coordinates to simplify trig functions.
The quadrant of an angle determines the sign (positive/negative) of sine, cosine, and tangent.
Works Cited
Math Monks. “Unit Circle (in Degrees & Radians) – Definition, Equation, Chart.” MathMonks, https://mathmonks.com/circle/unit-circle.
Lumen Learning. “Unit Circle: Sine and Cosine Functions.” Lumen Learning, https://courses.lumenlearning.com/precalculus/chapter/unit-circle-sine-and-cosine-functions/.
BetterExplained. “Intuitive Guide to Angles, Degrees, and Radians.” BetterExplained, https://betterexplained.com/articles/intuitive-guide-to-angles-degrees-and-radians/.
Brain, Marshall. “How to Use the Unit Circle in Trigonometry.” HowStuffWorks, https://science.howstuffworks.com/math-concepts/unit-circle.htm.