Trigonometry Review

Functions

List of the 6 Functions used in Trigonometry

• sin(x)
• cos(x)
• tan(x)
• csc(x)
• sec(x)
• cot(x)

Trigonometric Functions in relation to the sides of a triangle

• sin(θ) = opposite / hypotenuse
• cos(θ) = adjacent / hypotenuse
• tan(θ) = opposite / adjacent
• csc(θ) = hypotenuse / opposite
• sec(θ) = hypotenuse / adjacent
• cot(θ) = adjacent / opposite

Trigonometric Functions

Introduction

Trigonometric functions describe the relationships between the angles and the side lengths of triangles, particularly right triangles. They are essential for studying periodic motion, waves, circular relationships, and circular motion.

There are six main trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot).

Each of these functions can be defined in two ways:

• In a right triangle, based on the ratio of specific sides.
• On the unit circle, where they are defined for all real angles.

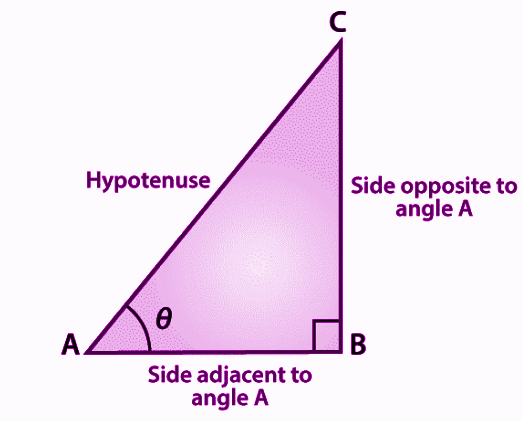
Right Triangle Definitions

In a right triangle with an acute angle θ:

• sin(θ) = opposite / hypotenuse
• cos(θ) = adjacent / hypotenuse
• tan(θ) = opposite / adjacent

Visualizing the Functions

You can remember the right-triangle relationships with the acronym SOH-CAH-TOA:

• Sine = Opposite / Hypotenuse
• Cosine = Adjacent / Hypotenuse
• Tangent = Opposite / Adjacent

Include a simple diagram of a right triangle with the sides labeled “opposite,” “adjacent,” and “hypotenuse” to help visualize each function.

Trigonometric Functions on the Unit Circle

While the triangle definitions only apply to acute angles, the unit circle definition extends trigonometric functions to all real numbers.

On a unit circle centered at (0, 0) with radius 1:

• cos(θ) = x
• sin(θ) = y
• tan(θ) = y / x (when x ≠ 0)
• csc(θ) = 1 / y (when y ≠ 0)
• sec(θ) = 1 / x (when x ≠ 0)
• cot(θ) = x / y (when y ≠ 0)

This means the coordinates of a point on the unit circle directly represent the values of sine and cosine for any given angle θ.

Quadrants and Sign Rules

Quadrant	Sine	Cosine	Tangent
I (0°–90°)	+	+	+
II (90°–180°)	+	-	-
III (180°–270°)	-	-	+
IV (270°–360°)	-	+	-

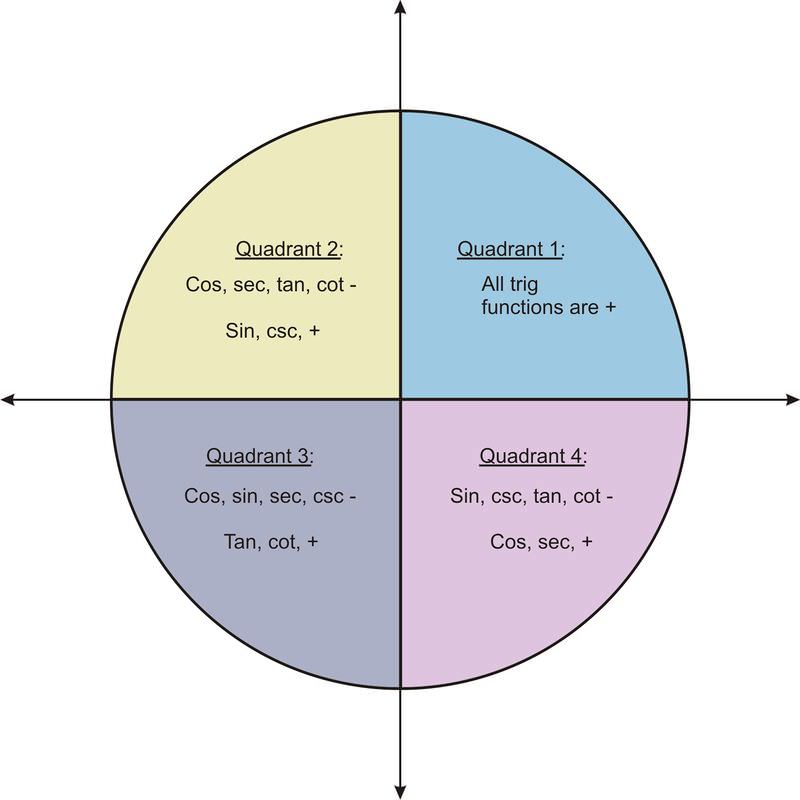
A common phrase to remember: “All Students Take Calculus”

• A = All functions positive (Quadrant I)
• S = Sine positive (Quadrant II)
• T = Tangent positive (Quadrant III)
• C = Cosine positive (Quadrant IV)

Example Problems

1. Find sin 30°, cos 30°, and tan 30°

• sin(30°) = 1/2
• cos(30°) = sqrt(3) / 2
• tan(30°) = 1 / sqrt(3)

2. Find sin(pi/4) and cos(pi/4)

• sin(pi/4) = sqrt(2) / 2
• cos(pi/4) = sqrt(2) / 2

3. Find tan(3pi/2)

On the unit circle, (x, y) = (0, -1)

tan(3pi/2) = -1 / 0 → Undefined

Applications of Trigonometric Functions

• Modeling sound and light waves
• Describing periodic motion (pendulums, springs, etc.)
• Navigation and surveying
• Architecture and computer graphics
• Electrical engineering (AC currents and phase shifts)

Summary

• The six trigonometric functions define relationships between sides and angles of triangles.
• On the unit circle, sine and cosine correspond to the x and y coordinates.
• Tangent and its reciprocal functions describe slopes and ratios.
• Understanding the signs in each quadrant is important for working with angles beyond 90°.